4-bit DAC using op-amp
For interfacing the digital circuit with the analog circuit, we must be able to convert the digital signal into an analog signal and the analog signal into a digital signal.
If there is a digital output and we need an analog output, we need to convert the digital signal into an analog signal. DAC (Digital-to-Analog Converter) takes digital inputs and generates the output, which is equivalent to the analog signal.
There are many circuits to convert the digital signal into an analog signal. One of them is using the op-amp summing amplifier. Let us recall the Summing Amplifier.The figure shown below is the connection for the summing amplifier.
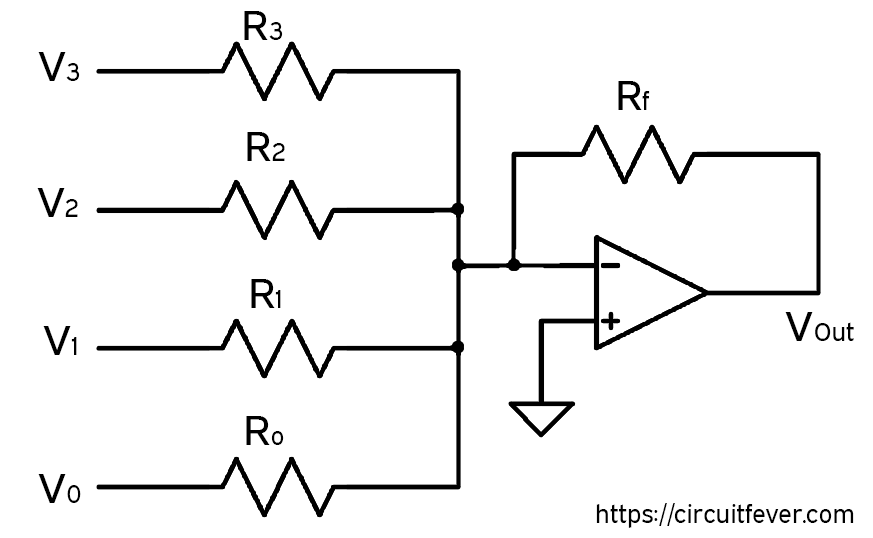
Output of this circuit is given by:
$$ V_{out}=-\left\{ \frac {R_f}{R_0}V_0+\frac {R_f}{R_1}V_1+\frac {R_f}{R_2}V_2+\frac {R_f}{R_3}V_3 \right\} $$
In this circuit, if
$$R_f=R_0=R_1+R_2=R_3=R$$
Then output becomes
$$v_{out}=-(V_0+V_1+V_2+V_3)$$
It is the sum of input voltages.
Please note that the negative sign only indicates the inverting amplifier.
We can use this circuit to convert the digital signal into an analog signal. A circuit diagram for a DAC using an op-amp is shown below:
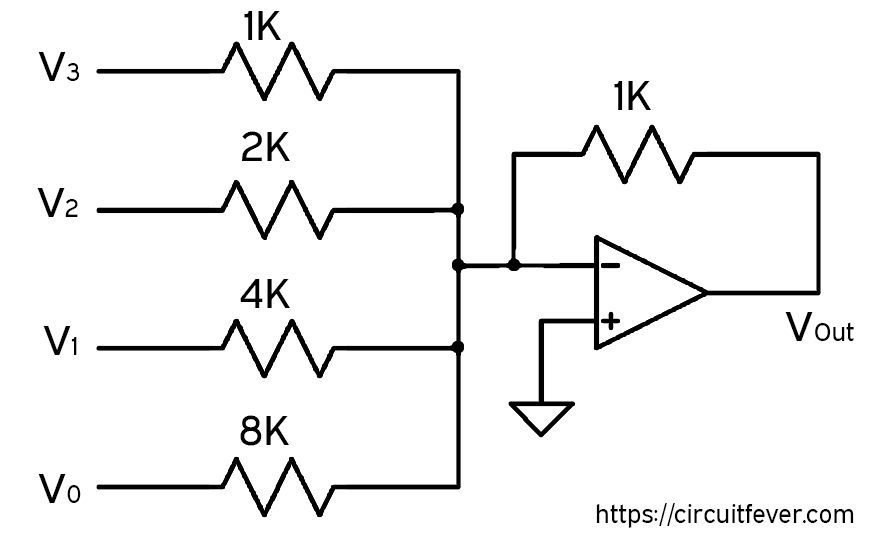
In this circuit, V0, V1, V2, and V3 are for digital inputs. We have replaced the resistors of the value given below:-
$$R_3 \rightarrow 1 K\Omega $$
$$R_2 \rightarrow 2 K\Omega $$
$$R_1 \rightarrow 4 K\Omega $$
$$R_0 \rightarrow 8 K\Omega $$
and also, feedback resistor
$$R_f \rightarrow 1 K\Omega $$
So that the output of the circuit becomes
$$V_{out}=-(V_3+\frac 12V_2+\frac14V_1+\frac18V_0)$$
(Negative sign only represents inverting apmlifier and we are not considering polarity).
Let us consider that the full-scale voltage of binary 1 is 5V, and for binary 0 is 0V. If binary input is "1001", then the output voltage becomes:
$$V_{out}=-(5+0+0+0.625)V=5.625V$$
The output of this circuit for different digital inputs is given below:
| A | B | C | D | Vout |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | -0.625 |
| 0 | 0 | 1 | 0 | -1.250 |
| 0 | 0 | 1 | 1 | -1.875 |
| 0 | 1 | 0 | 0 | -2.500 |
| 0 | 1 | 0 | 1 | -3.125 |
| 0 | 1 | 1 | 0 | -3.750 |
| 0 | 1 | 1 | 1 | -4.375 |
| 1 | 0 | 0 | 0 | -5.000 |
| 1 | 0 | 0 | 1 | -5.625 |
| 1 | 0 | 1 | 0 | -6.250 |
| 1 | 0 | 1 | 1 | -6.875 |
| 1 | 1 | 0 | 0 | -7.500 |
| 1 | 1 | 0 | 1 | -8.125 |
| 1 | 1 | 1 | 0 | -8.750 |
| 1 | 1 | 1 | 1 | -9.375 |
Clearly, the output of this circuit is equal to the weighted sum of the digital inputs. The full-scale value of this circuit is (-9.375V). The output of this circuit depends on two factors: the value of the feedback resistor and the precision of the input voltage.
