Carry Look Ahead Adder
Carry Look Ahead Adder is digital circuit which performs n-bit addition operation. Here we only use generator and propagator to computes carry out. We knows that boolean expression for carry out of a full adder is given by: $$C_{out} = AB + (A \oplus B)C_{in}$$
Let's reformulating carry out equation and try to understand why we are doing like this.
Ripple Carry Adder
For n-bit addition opereation, ripple-carry adder is the basic digital circuit in which we use n number of for adder for performing n-bit addition operation. But the problem in ripple carry adder is the propagation delay. The next full-adder output is dependent on carry output of previous addition operation. More number of operand bits is more propagation delay and less parallel operation.
Full Adder Truth Table
| A | B | Cin | AB | A⊕B | Cout |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 | 1 |
Truth table of a full-adder is given in above table. When A⊕B is 1, carry is propagated and when AB is 1, carry is generated. Let's replace A AND B with G (generator)and A EX-OR B with P (propagator). Then the carry out equation becomes. $$C_{out} = G +PCin$$
We can also replace Ex-or operation with OR operation. It can also computes the carry out $$C_{out} = AB + (A + B)C_{in}$$
Carry Out Equation
Now we can write the carry out equation in terms of generator and propagator $$C1 = g0 + p0 C_{in}$$ $$C2 = g1 + p1 C1$$ $$C3 = g2 + p2 C_{2}$$ $$C4 = g3 + p3 C3$$ Let's expand these equations $$\boxed{C1 = g0 + p0 C_{in}}$$ Now C2 $$C2 = g1 + p1 C1$$ $$C2 = g1 + p1(g0 + p0 C_{in})$$ $$\boxed{C2 = g1 + g0p1 + p1p0 C_{in}}$$ Now C3 $$C3 = g2 + p2 C_{2}$$ $$C3 = g2 + p2 (g1 + g0p1+p1p0C_{in})$$ $$\boxed{C3 = g2 + g1p2 +g0p2p1 + p2p1p0 C_{in}}$$ Now C4 $$C4 = g3 + p3 C3$$ $$C4 = g3 + p3 (g2 + g1p2 +g0p2p1 + p2p1p0 C_{in})$$ $$\boxed{C4 = g3 + g2p3 + g1p3p2 + g0p3p2p1+p3p2p1p0C_{in}}$$
If we observe the carry out equation, there is no dependency on previous carry output for performing addition operation.This can perform fast and parallel addition operation.
Circuit Diagram
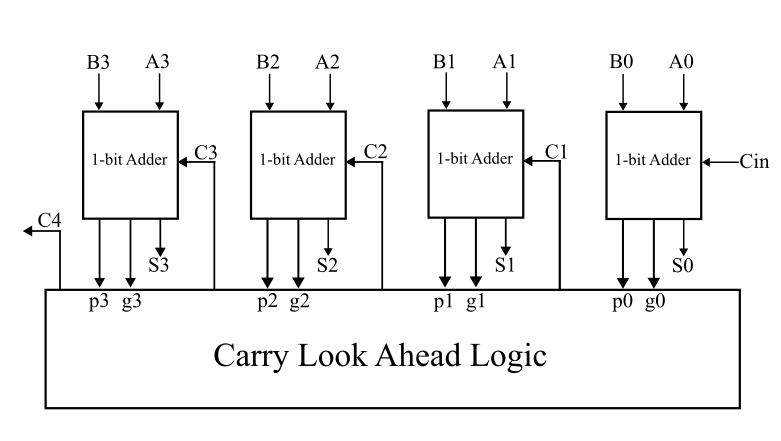
In above diagram, 4-bit carry look ahead adder is shown. The generator and propagator is computed from the full adder and parallel carry out is computed. This circuit performs fast and parallel addition operation.
