Full Adder Using Half Adder Verilog Code

Full adder is a combinational circuit which computer binary addition of three binary inputs. The truth table of full adder is given below.

We can write boolean expression for full adder as follows $$sum = a\oplus b \oplus cin$$ $$carry = a.b + b.cin + cin.a$$

If you see above equation, we require two ex-or gate, three AND gate and one three input OR gate. We can minimise the logic gate requirement by modifying the boolean expression as follows. $$carry = ab + (a \oplus b)cin$$

Now we require only two AND gate and one OR gate in carry expression because a ex-or b is already computed from sum expression. Now the logic gate required for implementing full adder is reduced.

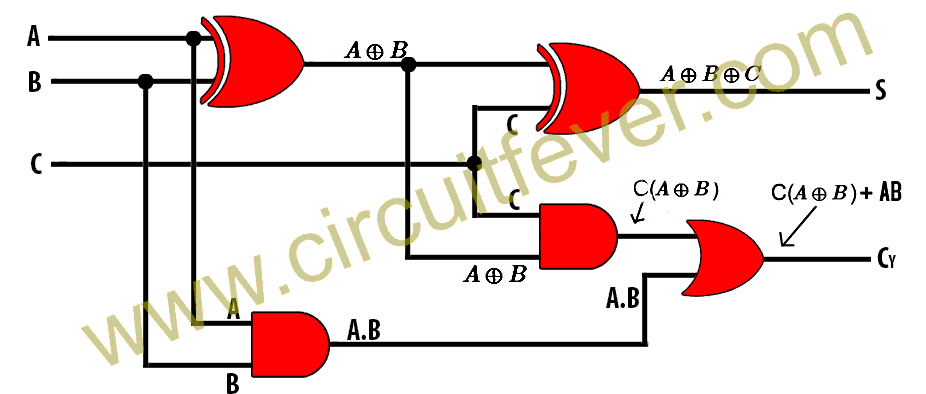
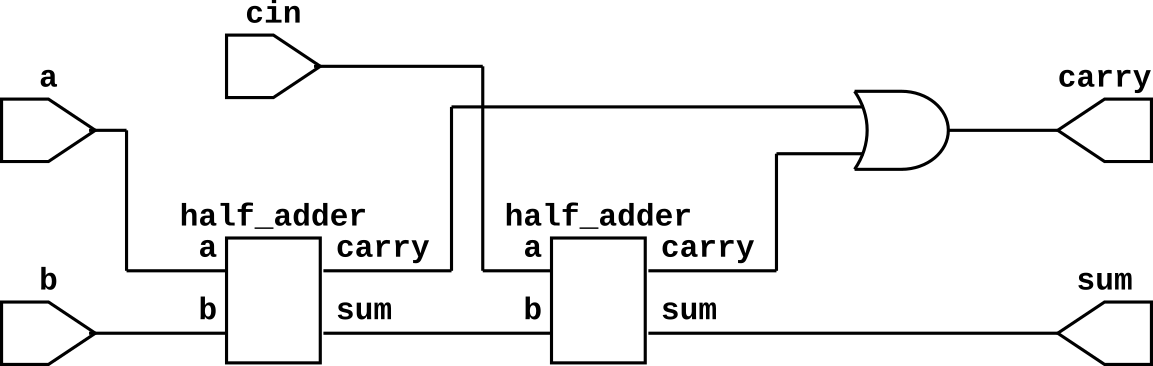
If you observe above boolean expression and logic ccircuit diagram, it is basically two half adder and one OR gate. $$\text{For a half adder, } sum = a \oplus b \text { and } carry = a.b$$ Hence, we can implement full adder using two half adder with addition of one OR gate.

Full Adder Verilog Code

First, we'll describe a half adder by creating a module half_adder in Verilog source file. Below is the Verilog code for half adder.

//Half adder using data flow modeling
module half_adder (
    input a,b,
    output sum,carry
);

assign sum = a ^ b;
assign carry = a & b;

endmodule

Now create another seperate module for full adder. The module neme is full_adder and input output port list is same as full adder module. Instantiate two half adder with instance name ha0 and ha1. Make connection between the top module and half_adder module. The verilog code for full adder using half adder is given below.

//Full adder using half adder
module full_adder(
    input a,b,cin,
    output sum,carry
);

wire c,c1,s;

half_adder ha0(a,b,s,c);
half_adder ha1(cin,s,sum,c1);

assign carry = c | c1 ;

endmodule

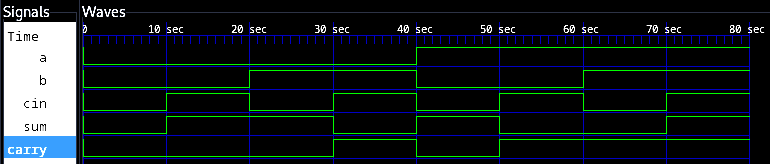
Full Adder Testbench

module full_adder_tb;
reg a,b,cin;
wire sum,carry;

full_adder uut(a,b,cin,sum,carry);

initial begin
a = 0; b = 0; cin = 0;
#10
a = 0; b = 0; cin = 1;
#10
a = 0; b = 1; cin = 0;
#10
a = 0; b = 1; cin = 1;
#10
a = 1; b = 0; cin = 0;
#10
a = 1; b = 0; cin = 1;
#10
a = 1; b = 1; cin = 0;
#10
a = 1; b = 1; cin = 1;
#10
$finish();
end
                
endmodule