Kirchhoff's voltage law (KVL) and Kirchhoff's current law (KVL) are two fundamental law to find voltage and current in an electrical circuit.
We know that voltage remains the same in the resistor connected in parallel with the source voltage and current remain the same in each resistor connected in series with the supply current.

Voltage divides in reach resistors when it is connected in series with the supply voltage. Similarly,
Current divides in each resistors when it is connected in parallel with the supply current.

We can understand this better by considering two resistors and applying the KCL and KVL.

Voltage Division

Let us consider a simple circuit containing two resistors connected in series with the supply voltage V. According to the Kirchhoff's voltage law (KVL) sum of the voltage drop across the resistors are equal to the supply voltage.
$$V_1+V_2=V$$

But, what is the value of voltage drop across both of the resistors? We can find this by solving the KVL equation.

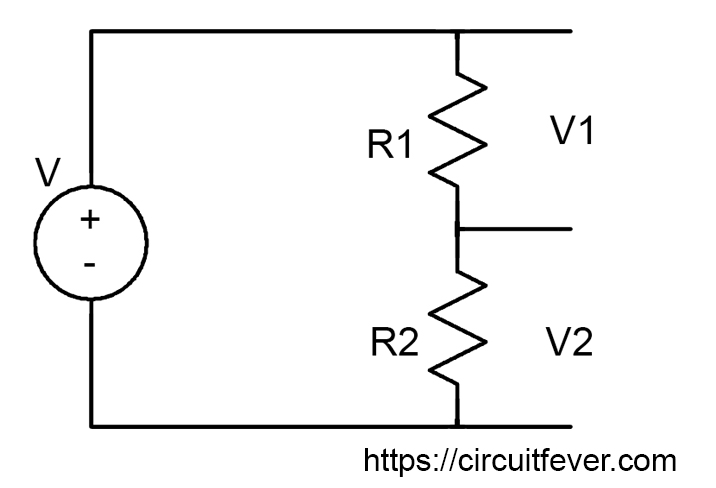
But here is a trick you'll find useful. Multiply the resistor that you want to find voltage across that resistor with the supply voltage and finally divide with the sum of both the resistors.

$$V_1 = V\times \frac{R_1}{R_1+R_2}$$

$$V_2 = V\times \frac{R_2}{R_1+R_2}$$

If you use this rule, you don't have to solve KVL equation again and again for this type of circuit.

Current Division

Again, let us consider a circuit in which both the resistors are in parallel with the input source. For simplicity I've given an independent current source.

According to the Kirchhoff's Current Law (KCL), incoming current is equal to outgoing current.
$$I_1+I_2=I$$

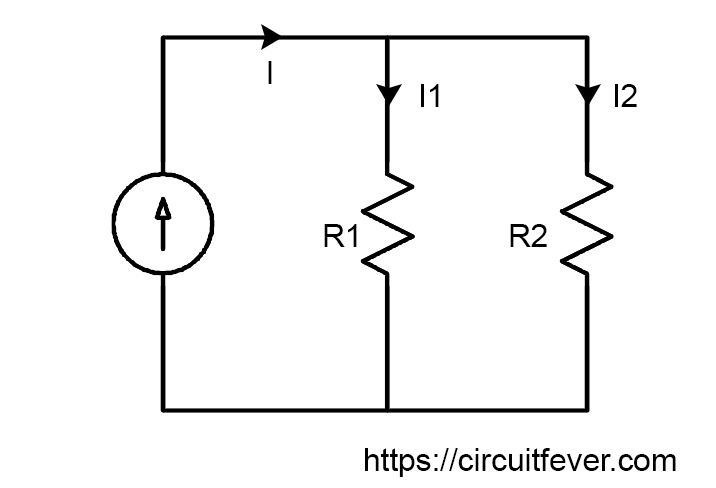
You can solve KCL equation to find I1 and I2. But, here is a trick.
Multiply resistance opposite to the resistance you want to find current flowing through them with the total current and finally divide with the sum of both resistance.

$$I_1 = I\times \frac{R_2}{R_1+R_2}$$

$$I_2 = I\times \frac{R_1}{R_1+R_2}$$

Use this trick and you'll save time in solving the circuit similar to the above circuit.